
|

|

|
|
a. face.nf50k.m
|
b. face.nf50k.uv.m
|
c. face.nf50k.pos.m
|
|

|

|
|
a. kitten.m
|
b. kitten.uv.m
|
c. kitten.pos.m
|
Algorithm Description
User specifies the target Gaussian curvature at each vertex. Euclidean Ricci flow computes a unique metric, which induces the
prescribed curvature. Current version is a simplified Euclidean Ricci flow algorithm, which aussmes the edge weight to be zeros by default.
Current version set all interior vertex curvature to be zeros, in practice, user can specify arbitrary target curvatures for them.
For example, user can concentrate all curvatures at a special vertex, or uniformly at all vertices. The target curvature can be dynamic
during the optimization also.
Input and output
If the input mesh is a topological disk as shown in the figure, the only input is
- a genus zero mesh with a single boundary, e.g. face.nf50k.m
- Current version sets the target curvature at the interior vertices to be zeros; the boundary vertex curvature
equals to 2PI/n, where n is the total number of boundary vertices.
The output is
- The mesh with uv coordinates determined by the target flat metric, e.g.face.nf50k.uv.m
|
|
|
|
a. kitten.open.m view 1
|
b. kitten.open.m view 2
|
c. kitten.open.m view 3
|
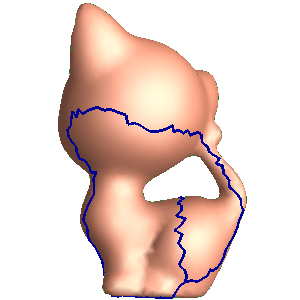
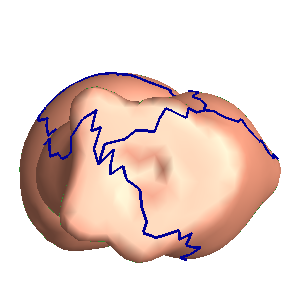
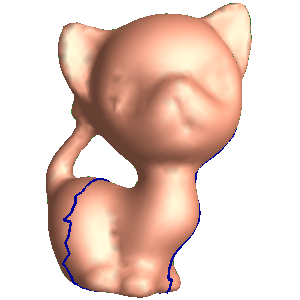
If the input mesh is a high genus mesh with complicated topolyg, the inputs are
- a high genus mesh, e.g. kitten.m
- the fundamental domain of the mesh, e.g.kitten.open.m
- Target curvature. For genus one closed mesh, the target curvature is set to be zero everywhere.

|
|
Plannar image of the kitten mesh with flat metric, 3 periods are shown by shifiting kitten.pos.m.
|
The output is
- The mesh with uv coordinates determined by the target flat metric, e.g.kitten.uv.m By shifting
the planar image of the mesh, the whole plane can be consistently tessellated, e.g. three periods of the kitten image are
illustrated in the above figure.
Command
For face mesh
EuclideanRicciFlow.exe face.nf50k.m face.nf50k.uv.m
For Kitten mesh
cutgraph.exe kitten.m kitten.cut.m
slice.exe kitten.cut.m kitten.open.m
EuclideanRicciFlow.exe kitten.m kitten.open.m kitten.uv.m
Target Curvature
Target curvature can be set by the user, as long as the total target curvature is 2PI times Euler number of the mesh.
Convergence and Stability
The stability is mainly determined by the connectivity of the mesh. In theory, if the target curvature
is outside the admissible curvature space of the mesh, then the program will terminate abnormally. In order to ensure
the target curvature to be admissible, the following hints are useful:
- The number of faces attaching to a vertex is called the vertex valence. The vertex valence should be greater than
2(2PI-K)/PI, where K is the target curvature.
- Special attention needs to be paid to boundary vertices. Remove all valence 1 boundary vertices.
Example
The input face mesh has 50k faces. The computational time is about 10 seconds on a PC with 3.0 GB of RAM, 3.60 GHz CPU.
The data set and the source can be downloaded.










