Algorithm Description

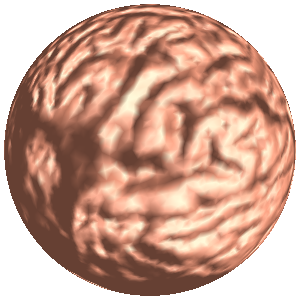
Spherical harmonic map computes a harmonic map from a topological sphere to the unit sphere in three dimensional Euclidean space. In theory, harmonic maps between topological spheres are conformal. The harmonic maps are not unique, two such maps differ by a Mobius transformation of the unit sphere. More constraints, such as the correspondances between feature points, feature curves can be easily added to the algorithm. The algorithm depends on the initial map. Any degree one map (may not be a homeomorphism) can be used as the initial map. By nature, the algorithm is tangential gradient descend method, which is highly non-linear. User needs to control the step length and the termination condition by setting the error tolerance.

Input and output

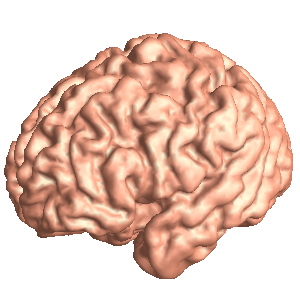
• The input is a genus 0 closed mesh, as shown in the top row.
• The output is the image of the spherical harmonic mapping, as shown in the bottom row.

Command

   spherical_harmonic_map.exe brain.m brain.sphere.m

Initial Map

   The initial map is the Gauss-Map.

Convergence, Stability and Efficiency

   The computational convergence and stability are affectly greatly by the following factors:

• Initial mapping. For simple shapes, Gauss-map is good enough. For complicated shapes, the computation process may get stuck in the local minimum of harmonic energy. One way to avoid local minimum is as follows. First, we divide the mesh to two topological disks. Then use disk harmonic map to map each segment to the unit disk. By using stereo-graphic projection, we map each segment to a hemisphere. Make sure the consistency between the images of two boundaries. Then we can map the mesh to the unit sphere in a one-to-one manner. Use this map as the initial map, and run spherical harmonic mapping algorithm, we can reach the global minimum of harmonic energy.
• Quality of the triangulation. It is highly desirable to reduce the number of obtuse corner angles.
• Step length. In the optimization process, if the step length is too big, then the computaiton is unstable; if the step length is too small, the process is too slow.

Example

   The input brain mesh has 30k faces. The computational time is 65 seconds on a PC with 3.0 GB of RAM, 3.60 GHz CPU. The data set and the source can be downloaded.