|

|
|

|
|
face.nf25k.m
|
face.nf25k.open.m
|
face.nf25k.pos.m
|
face.nf25k.uv.m
|

|

|

|

|
|
face.2cut.m
|
face.2cut.open.m
|
face.2cut.pos.m
|
face.2cut.uv.m
|
|
|
|

|
|
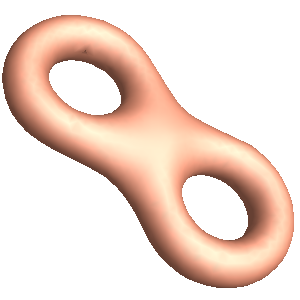
eight.m
|
eight.open.m
|
eight.pos.m
|
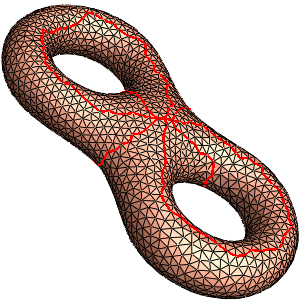
eight.uv.m
|
Algorithm Description
Compute hyperbolic metrics of meshes with negative Euler numbers. If the surfaces are with boundaries, then the boundaries
are mapped to hyperbolic lines, namely the curvature of boundary vertices are also zeros.
Input and output
The input meshes are
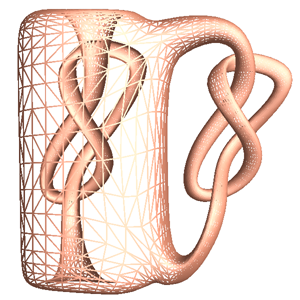
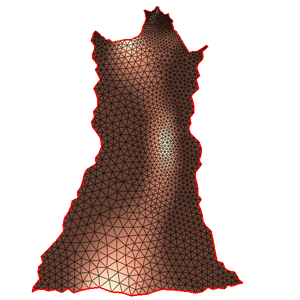
- A mesh with negative Euler number, e.g. face.nf25k.m.
- A fundamental domain of the mesh, e.g. face.nf25k.open.m.
The output is the mesh with uv coordinates,
- mesh with uv coordinates, which is the isometric embedding of the fundamental domain in Poincare disk,
induced by the hyperbolic metric face.nf25k.uv.m.
The univeral covering space of the input mesh equipped with the hyperbolic metric can be isometrically embedded on the Pioncare disk,
the fundamental domains form a tessellation of the Poincare disk as shown in the above figure.
Convergence, Stability and Efficiency
The computational process is stable and converges fast.
Example
The input face mesh has 25k faces, 3 boundaries. The computational time is about 8 seconds on a PC with 3.0 GB of RAM, 3.60 GHz CPU.
The data set can be downloaded. Please contact David Gu for the source code.
Command
- Compute the cut graph:
cutgraph.exe eight.m eight.cut.m
- Compute the fundamental domain:
slice eight.cut.m eight.open.m
- Compute the hyperbolic metric:
hyperbolic_ricci_flow.exe eight.m eight.open.m eight.uv.m
The output is
eight.uv.m
For face meshes, the cut graph can be computed using slitmap.exe.