eight.open_0.m	eight.open_1.m	eight.open_2.m	eight.open_3.m
eight.u_0.m	eight.u_1.m	eight.u_2.m	eight.u_3.m

Algorithm Description

Harmonic 1-form algorithm computes harmonic 1-forms on a high genus closed surface. According to Hodge theory, each cohomologous class has a unique harmonic form. The algorithm is linear.

eight.m

Input and output

There are two input meshes:

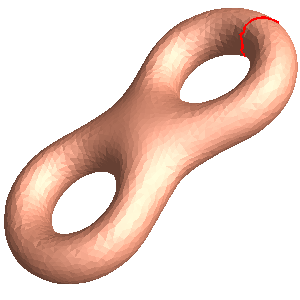
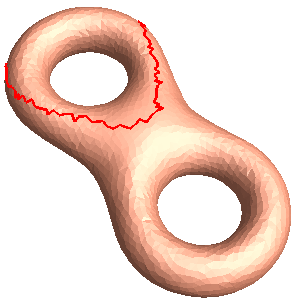
• A high genus closed mesh, e.g. the genus two eight.m.
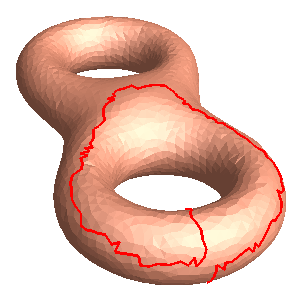
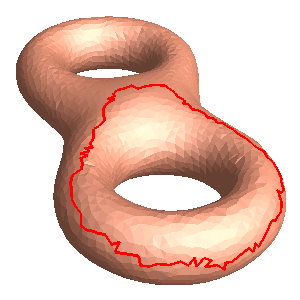
• The mesh is sliced open along a homology basis loop, e.g. eight.open_0.m.

• The closed mesh with harmonic 1-form recorded as edge traits eight.w_0.m.
• The mesh cut along the homology basis with uv coordinates, which are obtained by integrating by the harmonic 1-form, e.g. eight.u_0.m.

Convergence, Stability and Efficiency

The computational process is stable and converges fast.

Example

   The input genus two mesh has 7k faces. The computational time is about 2 seconds on a PC with 3.0 GB of RAM, 3.60 GHz CPU. The data set and the source can be downloaded.

Command